Landslides: Slope stability, triggers, failure dynamics, and morphology
Contents [show]
Introduction
This report provides a brief overview of the physics of landslides and overviews many types of landslides and triggers, with a focus on landslides triggered by earthquakes. I focus only on terrestrial landslides and do not consider subaqueous landslides.
Why Study Landslides?
The economic and human losses related to landslides are significant. In the United States alone, 25 to 50 lives are lost each year due to landslides and repairs after landslides occur require 1 to 3 billion dollars to repair (National Academies, 2004). A harsh reminder of the devastating effects of landslides occurred in Oso, Washington in 2014 when a hillside collapsed, destroying a neighborhood and killing 43 people. However, the effects of an extensive landsliding event, such as one triggered by an earthquake dwarf the detrimental effect of a single landslide. Between 1968 and 2008, earthquake induced landslides were responsible for over 70,000 deaths (Marano, 2009). The landslides triggered by the 2008 Wenchuan earthquake alone were responsible for more than 20,000 of these fatalities (Chuan Tang, 2011).
While some potential slides can be predicted and stabilized, the majority cannot. Widespread stabilization is not feasible, especially on a global scale. Instead, we rely on hazard mapping to identify vulnerable areas. Accurate hazard maps depend on knowledge of landslide dynamics, physical conditions, and forcings (such as increased precipitation or shaking from an earthquake).
Slope Stability
Slope stability is dependent on the following:
- Material involved including:-Material properties (cohesion and the internal friction)-Fracture density and quality-Weathering of the material
- Geometry of material
- Slope angle
- Weight distribution
- Water content
- Vegetation
- External impulsive forces (such as earthquakes)
Factor of Safety
Thefactor of safety of a slope describes the stability of the slope and is a ratio of the resisting forces to driving forces. A factor of safety greater than one indicates a stable slope. There are multiple methods for calculating the factor of safety of a slope. The calculation of the safety of a sliding block on a plane (a layered slide with preferential failure along pre-existing weaknesses) is shown below in figure 1. This calculation takes into account slope angle, friction, cohesion, and water content. Increasing water content and slope angle decreases the factor of safety. Increasing friction and cohesion increases the strength and therefore increases the factor of safety. The sliding plane calculation of the factor of safety cannot be applied to homogenous soils where there is no preferential weak layer for failure. The failure surface in homogenous soils is sub-spherical, resulting in a rotational slide.
Figure 1: Factor of safety calculation. Figure from Marin Clark (personal communication).
Material properties control the strength of a rock or soil and are an important control on the type of failure. The intrinsic strength of a rock or soil comes from cohesive strength and the internal friction. Cohesion is the resistance force per unit area, and is measured in Pascals. In fine-grained soils, cohesion is a result of electrostatic bonds between clay and silt particles and is on the order of a few KPa. Sands and gravels are effectively cohesion-less. Rock has much greater cohesion due to interlocking particles and cement. Cohesion values for rock may be 1000s of times larger than those of soils (De Blasio, 2011). The internal friction of a soil or rock is due to the frictional forces between grains, and is often represented as the internal angle of friction, Φ. The internal angle of friction depends on grain size and grain properties, and can range from 0 to 45. Sandy soils and gravels generally have a friction angle between 30 and 40 degrees, while clayey soils tend to have a friction angle up to about 35 degrees. These values are generalizations and do not apply to all soils in these catagories (Koloski et al, 1989).
The cohesion and internal angle of friction can be determined for small samples in the lab using a tri-axial compression test or a uniaxial compression test (among others). Small-scale tests can also be used to measure the strength of individual discontinuities. However, these small-scale tests do not take into account the large-scale heterogeneities encountered in the field, such as variable weathering, fractures, jointing, and bedding. Large-scale heterogeneities often control the initiation and location of failure. Multiple failure criterions to evaluate the stability of a slope accounting for large-scale discontinuities have been developed. All require careful study of a field site, and are difficult to apply broadly.
The above factor of safety calculation does not take into account the geometry of the slope, the distribution of weight, or the vegetation. Geometry of a slope includes the strike and dip of the potential failure planes (bedding, joints, etc) and the orientation of the failure planes with respect to the slope. Discontinuities that "daylight" and are dipping at a lower angle than the slope angle are capable of failure along the weakness plane. Planes that are steeper than the slope slope angle will not slide, though they may undergo toppling failure.
Changes in the center of gravity of a potential failure can trigger failure or serve to stabilize a slope. Adding weight to the top of a potential failure will decrease stability while adding weight to the base of the same potential failure can increase stability. The role that weight distribution plays is also dependent on geometry of the slope. Vegetation generally serves to stabilize a slope; the roots of plants serve as anchors, and vegetation decreases the water content of a slope. However, vegetation also adds weight to a potential slide, and can decrease stability.All of these factors must be evaluated for each potential slide, and considered when analyzing a slide that has already occurred.
Landslide triggers
A landslide trigger decreases the factor of safety to less than one. When the factor of safety is less than one, driving forces are greater than resisting forces, and failure will occur. Triggers include both natural and human-caused events. Human induced triggers include removal of the toe of the landslide through excavation, loading of the head of the landslide (addition of mass), and artificial vibration. Natural triggers include toe removal through erosion, changes in water pressure, and earthquakes. Any of these potential triggers can also combine to cause failure (Waltham, 1994).
Water Pressure
Increasing water levels is the most common trigger of landslides. Increased water pressure decreases the effective stress and the factor of safety of a slope. The Oso landslide in Washington was likely triggered by increased precipitation in the weeks before the slide occurred (Henn et al, 2015). Precipitation can also trigger landslides destabilized by a previous event such as an earthquake, as seen in the landslides triggered by a rainstorm after the Wenchuan earthquake (Tang et al, 2011).
Earthquake triggers
Earthquakes cause failure in two different manners. The vibration from an earthquake can cause liquefaction in uniformly graded, fine-grained, sediments due to loss of effective stress. Earthquakes can also increase the shear stress on a slope, decreasing the factor of safety to below one (De Blasio, 2011). According to Newmark analysis (Newmark, 1965), displacement and landsliding occurs when a critical acceleration is reached. The critical acceleration for failure can be calculated using the following equation:![]() where ac is the critical acceleration, g is acceleration due to gravity and alpha is local slope.
where ac is the critical acceleration, g is acceleration due to gravity and alpha is local slope.
Large, shallow earthquakes frequently trigger landslides. Work from Keefer (1984) suggests that an earthquake as small as a magnitude 4.0 can trigger failures. The smallest earthquakes (ML (Richter local magnitude) = 4.0) can trigger rock falls, rockslides, soil falls, and soil slides. The largest earthquakes (Ms (Richter surface wave magnitude)≥ 6.5 can trigger rock and soil avalanches. The area affected by landsliding is also dependent on earthquake magnitude (see figure 2). As magnitude increases, the extent of landsliding increases. An example of the extensive area that can be effected by landsliding during an earthquake is shown in figure 3 below. Figure 3 shows the distribution of landslides from the magnitude 6.7 1994 Northridge earthquake. Around 10,000 km2 was effected by landsliding, matching predictions made by Keefer (see figure 2).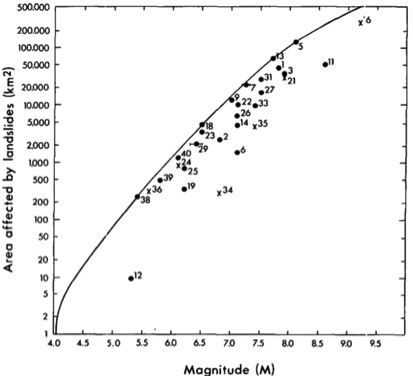
Figure 2: The relation between earthquake magnitude and the area affected by landslides. Figure is from Keefer (1984).
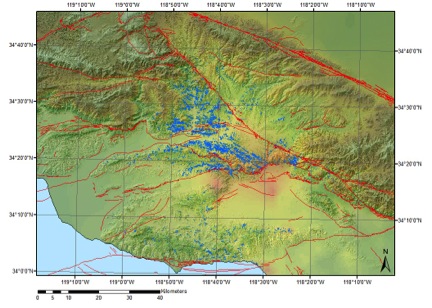
Figure 3: An example of the distribution of earthquake triggered landslides after the 1994 Northridge earthquake.Landslides (Harp and Jibson, 1996) are blue polygons and active quaternary faults (USGS and CGS, 2006) are the red lines.
Modeling the effects of an earthquake on a hillslope
There have been many attempts to model the effects an earthquake has on a slope to assess the likelihood of failure in a given event. Jibson (2011) overviewed three of the methods used, pseudostatic analysis, stress-deformation analysis, and the Newmark sliding block analysis.
Pseudostatic Analysis
Pseudostatic analysis assumes that the shaking from the earthquake can be represented as a permanent body force applied to a slope. The factor of safety is calculated using the equation below:![]() W is the weight per unit slope, alpha is the slope angle, phi is the internal angle of friction, and k is the pseudostatic coefficient. The pseudostatic coefficient is the horizontal ground acceleration divided by acceleration due to gravity. Any ground acceleration that causes the factor of safety to decrease below one will trigger failure according to this analysis. The diagram from Jibson (2011) below shows a force diagram used in pseudostatic analysis.
W is the weight per unit slope, alpha is the slope angle, phi is the internal angle of friction, and k is the pseudostatic coefficient. The pseudostatic coefficient is the horizontal ground acceleration divided by acceleration due to gravity. Any ground acceleration that causes the factor of safety to decrease below one will trigger failure according to this analysis. The diagram from Jibson (2011) below shows a force diagram used in pseudostatic analysis.

The representation of an earthquake as a single, continuous force on a slope is not accurate. Using the pseudostatic method to predict slope stability is often conservative, but in special cases where pore pressure will build up or shear strength will be lost during shaking, the analysis is unconservative. Essentially, pseudostatic analysis is a very basic analysis, and does not give any information about what occurs after the slope is no longer in equilibrium. However, due to its ease of use, and low cost, it can serve as a simple index of stability.
Stress-Deformation analysis
Stress-deformation analysis uses finite-element modeling methods to model the response of a slope to a stress. It uses a mesh and calculates the deformation of each node in response to the modeled stress. Quality of the model is determined by the quality of input data. High quality and high-density data are needed for the model to be accurate, and if the data is good enough, stress-deformation modeling will give the most accurate depiction of what occurs during shaking. However, as acquiring the necessary data needed is very expensive, stress-deformation analysis is typically only used for critical slopes and structures.Newmark analysis
Newmark analysis models landslides as a rigid block on an inclined plane. The critical acceleration is the acceleration needed to overcome basal resistance. To determine the displacement of a block, the acceleration record from an earthquake greater than the critical acceleration is integrated to produce a velocity-time function, which is then integrated to produce an estimate of the displacement. The interpretation of the displacement varies. Typically, a threshold displacement is assumed, such as 5 or 10 cm. Any displacements that exceed the threshold are predicted to fail.Newmark displacement assumes that the landslide experiences no internal deformation and moves as a rigid block during the entire failure. It also assumes that the critical acceleration remains constant and there are no dynamic pore pressure effects. Analyses of both laboratory models and earthquake-induced landslides have confirmed that Newmark analysis is fairly accurate when slope geometry, soil and rock properties, and acceleration are known.
The stress-deformation analysis provides the most information about behavior, but is also the most expensive and work intensive technique, making it infeasible for widespread analysis. Newmark analysis bridges the gap between the two methods, being both inexpensive and providing better information than pseudostatic analysis. (Jibson, 2011)
Types of landslides
The mode of failure depends on the material type, the structure of the material (bedding, joints, and the orientation of these planes of weakness), and the slope. Different modes of failure can also combine in complex failures. Rocks tend to fail along pre-existing planes of weakness such as joints or bedding planes. Soils tend to fail in rotational slides along the radius of the sphere with the lowest factor of safety. They can also fail along planes of weakness, such as the interface between rock and soil.
Rock Failures
- Rockfall
- Occurs on steep slopes (greater than 40 degrees)
- Most abundant failure during earthquakes
- Mostly in heavily jointed or weakly cemented rocks
- Rock slides
- Failure along a pre-existing discontinuity
- Similar material to rockfalls
- Rock Avalanches
- Disintegrated landslide that can travel hundreds km per hour across low slopes
- Typically occur when there is a large amount of kinetic energy in the slide (falling from a height)
- Rock Slumps
- Similar to soil slumps (deep seated slides in very weak rocks)
Soil Failures
Compared to rocks, soils are more isotropic, and do not commonly have dominant weak layers. Instead of failing along a pre-existing plane of weakness, soils often fail along a sub-spherical shell where the lowest factor of safety occurs.
- Soil falls
- Similar to rockfall, but material involved is soil
- Disrupted soil slides
- Disintegrate during movement
- Most slide on basal shear surfaces at contact between bedrock and soil, some slide on boundaries between different soil layers
- Soil Avalanches
- Similar to disrupted soil slides, but faster moving and more disrupted
- Soil Slumps
- Curved basal shear surface, deep seated
- Soil block slide
- Movement along a planar surface, often deep seated
- Rapid soil flows
- Streams of soil grains that flow in a fluid-like manner at high velocities
- Debris flows
- Debris flows are a mixture of sediment and water.
- They are typically fast moving and pose a serious hazard due to their speed, transport of large boulders, and variable viscosity.
Failure
The physics of landslides during failure depend on the type of landslide. Coherent blocks behave differently from disrupted, incoherent slides, and saturated slides behave differently from dry slides. This section briefly overviews the effect of water on landslide dynamics, focusing on debris flows, and the failure process of rock avalanches.
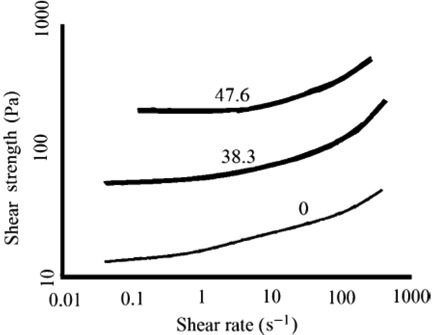 Theflowbehavior of a mudflow is modeled as a Bingham fluid. Bingham fluid flow consists of a basal shearing layer with velocity increasing until the boundary with an upper plug layer is reached. The upper plug layer moves at the same velocity as the top of the shearing layer. Figure 5 shows Bingham fluid flow on a slope. Channel morphology also controls the flow behavior, with decreasing channel volume increasing velocity, and increasing channel volume decreasing velocity.
Theflowbehavior of a mudflow is modeled as a Bingham fluid. Bingham fluid flow consists of a basal shearing layer with velocity increasing until the boundary with an upper plug layer is reached. The upper plug layer moves at the same velocity as the top of the shearing layer. Figure 5 shows Bingham fluid flow on a slope. Channel morphology also controls the flow behavior, with decreasing channel volume increasing velocity, and increasing channel volume decreasing velocity.
Failures that involve the transport of material, such as slides and flows, have three distinct parts, the source region, the run out region, and the deposition area. The source region is characterized by erosion, the run out region can be both erosional and depositional, and the deposition area is characterized by the deposition of the rock or sediment. The morphology of the depositional area is dependent on the type of failure. Disrupted failures can produce inverse grading, and compression ridges may appear when velocity in the center of the slide was greater than that on the sides of the slide. In cases where the slide moved as a coherent block, the block will be found in the depositional area with some internal deformation.
While distinguishing between the distinct failure parts in the field may be relatively simple, doing so for large scale mapping using aerial photography is difficult. Many landslide inventories have problems with landslide amalgamation, and do not differentiate between source areas and deposition. Accurate and complete landslide inventories are needed to train hazard models (See Coseismic landslide hazard mapping methodologies-Von Voigtlander). Incorporating the physics of landslide failure and transport will improve mapping of source areas and improve predictions of where landslides will occur and what they will impact.































6 COMMENTS
s. figuers*
Apr, 08, 2015 The title of this paper is earthquakes and landslides. The paper is a nice, short summary of landslide basics that can be found in any standard engineering geology textbook (I like the first equation). However, there is minimal discussion about landslides and earthquakes-your topic! What is different about how earthquakes cause landslides in soil or rock? (there are interesting differences) How common is it for earthquakes to reactivate existing standard landslides? There is a line of thought that earthquake cannot activate long landslides because only parts of the landslide are destabilized at any one time. Any thoughts about this? Do large earthquake landslides have an identifiable, thin failure surface (as do regular landslides)? Based on information from past earthquake landslide evaluations, is there any commonality about pre-existing causative factors (possible predictive factors)? What is the percentage of rock vs soil earthquake landslides (this is a rock mechanic course after all)? Katherine Lowe
Apr, 29, 2015 [quote name="s. figuers"]The title of this paper is earthquakes and landslides. The paper is a nice, short summary of landslide basics that can be found in any standard engineering geology textbook (I like the first equation). However, there is minimal discussion about landslides and earthquakes-your topic! What is different about how earthquakes cause landslides in soil or rock? (there are interesting differences) How common is it for earthquakes to reactivate existing standard landslides? There is a line of thought that earthquake cannot activate long landslides because only parts of the landslide are destabilized at any one time. Any thoughts about this? Do large earthquake landslides have an identifiable, thin failure surface (as do regular landslides)? Based on information from past earthquake landslide evaluations, is there any commonality about pre-existing causative factors (possible predictive factors)? What is the percentage of rock vs soil earthquake landslides (this is a rock mechanic course after all)?Dear S. Figuers,
You raise some interesting questions with answers I don't necessarily know. If you know of any papers I should read regarding your questions, I would greatly appreciate your suggestions.
The earthquake induced landslide inventories that I have worked with have limited information on material type as they are mostly mapped from aerial or satellite photography with limited fieldwork. As such, I don't know the relative percentages of rock verses soil landslides triggered by earthquakes.
Cheers,
Kate
Edit Comment
Ludger Suarez-Burgoa*
Apr, 09, 2015 Nowadays, engineers want also see a numerical implementation in some programming language as Python, Matlab, Octave or a similar one. Perhaps the author may do a simple numerical example with the infinite-planar slope model where earth quake influence is taken into consideration.In general I like the paper.
Katherine Lowe
Apr, 28, 2015 [quote name="Ludger Suarez-Burgoa"]Nowadays, engineers want also see a numerical implementation in some programming language as Python, Matlab, Octave or a similar one. Perhaps the author may do a simple numerical example with the infinite-planar slope model where earth quake influence is taken into consideration.In general I like the paper.
Dear Ludger Suarez-Burgoa,
Thank you for the suggestion. While I have limited programming experience currently, I will certainly take that into account for future work.
Cheers!
Kate
Edit Comment
vasiliki*
Apr, 09, 2015 Katherine,I think you made a very good effort in your report, but I would like you to elaborate a little bit more on the factors affecting slope stability. For instance, it would be great to add what is the factor that most affects landslide occurrence or any other statistical information. Also, what exactly do you mean by geometry of material and how is that different (or correlates) to slope angle?
The factor of safety definition refers to static conditions. Could you please include some information on how this is modified to take into account earthquake loading?
Could you also provide some typical values of friction angles for different soils?
Also, please provide some input with regards to figure 3.
Thank you and well done again!
Katherine Lowe
Apr, 28, 2015Dear Vasiliki,
Thank you for your comments and suggestions on my project. I have clarified what I meant by geometry and its relation to slope angle. I have also added a section on modeling the loading from an earthquake, including a brief overview of pseudostatic analysis, stress-deformation analysis, and rigid sliding block analysis. While these are obviously not all of the methods used to model the loading from an earthquake, I felt they were representative of the range of techniques used. I have also added a brief section on typical friction angles, though these are so variable for all of the various soil types that it is probably better to either look them up in a table or determine them site-by-site. The use of figure 3 to demonstrate landslide distributions was also clarified.
Cheers!
Kate
Edit Comment